Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

875, we get

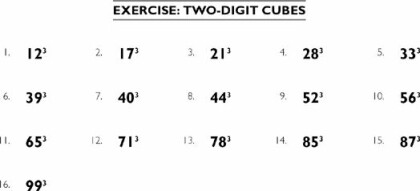
353 = 42,000 + 875 = 42,875

When cubing 49, we let d = 1 in order to round up to 50. Here

493 = (48 × 49 × 50) + (12 × 49)

We can solve 48 × 49 by the factoring method, but for this sort of problem, I prefer to use the close-together method, which will be described in Chapter 8. (Go ahead and look at it now, if you’d like!) Using that method, we get 48 × 49 = (50 × 47) + (1 × 2) = 2352. Multiplying this by 50, we get 117,600 and therefore

493 = 117,600 + 49 = 117,649

Here’s a larger one. Try the cube of 92.

923 = (90 × 92 × 94) + (22 × 92)

If you are fast at squaring two-digit numbers, then you could solve 92 × 94 = 932 − 1 = 8648, or you could use the close-together method, resulting in 92 × 94 = (90 × 96) + (2 × 4) = 8648. Multiplying this by 9 (as described in the beginning of Chapter 8), we obtain 9 × (8,600 + 48) = 77,400 + 432 = 77,832, and therefore 90 × 92 × 94 = 778,320. Since 4 × 92 = 368, we get

923 = 778,320 + 368 = 778,688

We note that when the close-together method is used for the multiplication problems that arise when cubing two-digit numbers, the small product being added will either be (depending on whether d = 1, 2, 3, 4, or 5) 1 × 2 = 2, 2 × 4 = 8, 3 × 6 = 18, 4 × 8 = 32, or 5 × 10 = 50. Let’s finish with the cube of 96.

963 = (92 × 96 × 100) + (42 × 96)

The product 92 × 96 = 8,832 can be done many different ways. To celebrate the end of this chapter, let’s do some of them. I’ll start with what I consider to be the hardest way, and end with what I consider the easiest way. By the addition method, (90 + 2) × 96 = 8,640 + 192 = 8,832; by the subtraction method, 92 × (100 − 4) = 9,200 − 368 = 8,832; by the factoring method, 92 × 6 × 4 × 4 = 552 × 4 × 4 = 2,208 × 4 = 8,832; by squaring, 942 − 22 = 8,836 − 4 = 8,832; by the close-together method with a base of 90, (90 × 98) + (2 × 6) = 8,820 + 12 = 8,832; and by the close-together method with a base of 100, (100 × 88) + (−8 × −4) = 8,800 + 32 = 8,832.

The product 42 × 96 = 1,536 can also be done a few different ways, such as 96 × 4 × 4 = 384 × 4 = 1,536, or as 16 × (100 − 4) = 1,600 − 64 = 1,536. Finally, since 8,832 × 100 = 883,200, we have

963 = 883,200 + 1,536 = 884,736

Chapter 4 Divide and Conquer: Mental Division

Chapter 4

Divide and Conquer:
Mental Division

Mental division is a particularly handy skill to have, both in business and in daily life. How many times a week are you confronted with situations that call on you to evenly divide things, such as a check at a restaurant? This same skill comes in handy when you want to figure out the cost per unit of a case of dog food on sale, or to split the pot in poker, or to figure out how many gallons of gas you can buy with a $20 bill. The ability to divide in your head can save you the inconvenience of having to pull out a calculator every time you need to compute something.

With mental division, the left-to-right method of calculation comes into its own. This is the same method we all learned in school, so you will be doing what comes naturally. I remember as a kid thinking that this left-to-right method of division is the way all arithmetic should be done. I have often speculated that if the schools could have figured out a way to teach division right-to-left, they probably would have done so!

ONE-DIGIT DIVISION

The first step when dividing mentally is to figure out how many digits will be in your answer. To see what I mean, try on the following problem for size:

179 ÷ 7

To solve 179 ÷ 7, we’re looking for a number, Q, such that 7 times Q is 179. Now, since 179 lies between 7 × 10 = 70 and 7 × 100 = 700, Q must lie between 10 and 100, which means our answer must be a two-digit number. Knowing that, we first determine the largest multiple of 10 that can be multiplied by 7 whose answer is below 179. We know that 7 × 20 = 140 and 7 × 30 = 210, so our answer must be in the twenties. At this point we can actually say the number 20 since that part of our answer will certainly not change. Next we subtract 179 − 140 = 39. Our problem has now been reduced to the division problem 39 ÷ 7. Since 7 × 5 = 35, which is 4 away from 39, we have the rest of our answer, namely 5 with a remainder of 4, or 5 and 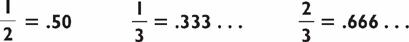. Altogether, we have our answer, 25 with a remainder of 4, or if you prefer, 25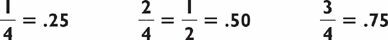. Here’s what the process looks like:

Let’s try a similar division problem using the same method of mental computation:

675 ÷ 8

As before, since 675 falls between 8 × 10 = 80 and 8 × 100 = 800, your answer must be below 100 and therefore is a two-digit number. To divide 8 into 675, notice that 8 × 80 = 640 and 8 × 90 = 720. Therefore, your answer is 80 something. But what is that “something”? To find out, subtract 640 from 675 for a remainder of 35. After saying the 80, our problem has been reduced to 35 ÷ 8. Since 8 × 4 = 32, the final answer is 84 with a remainder of 3, or 84⅜. We illustrate this problem as follows:

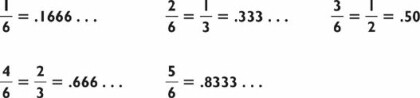
Like most mental calculations, division can be thought of as a process of simplification. The more you calculate, the simpler the problem becomes. What began as 675 ÷ 8 was simplified to a smaller problem, 35 ÷ 8.

Now let’s try a division problem that results in a three-digit answer:

947 ÷ 4

This time, your answer will have three digits because 947 falls between 4 × 100 = 400 and 4 × 1000 = 4000. Thus we must first find the largest multiple of 100 that can be squeezed into 947. Since 4 × 200 = 800, our answer is definitely in the 200s, so go ahead and say it! Subtracting 800 from 947 gives us our new division problem, 147 ÷ 4. Since 4 × 30 = 120, we can now say the 30. After subtracting 120 from 147, we compute 27 ÷ 4 to obtain the rest of the answer: 6 with a remainder of 3. Altogether, we have 236 with a remainder of 3, or 236¾.

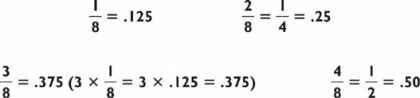
The process is just as easy when dividing a one-digit number into a four-digit number, as in our next example.

2196 ÷ 5

Here the answer will be in the hundreds because 2196 is between 5 × 100 = 500 and 5 × 1000 = 5000. After subtracting 5 × 400 = 2000, we can say the 400, and our problem has reduced to 196 ÷ 5, which can be solved as in the previous examples.

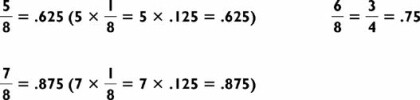
Actually, there is a much easier way to solve this last problem. We can simplify our problem by doubling both numbers. Since 2196 × 2 = 4392, we have 2196 ÷ 5 = 4392 ÷ 10 = 439.2 or . We’ll see more division shortcuts in the next section.

THE RULE OF “THUMB”

When dividing in your head instead of on paper, you may find it difficult to remember parts of the answer as you continue to calculate. One option, as you’ve seen, is to say the answer out loud as you go. But for greater dramatic effect, you may prefer, as I do, to hold the answer on your fingers and say it all together at the end. In that case, you may run into problems remembering digits greater than five if, like most of us, you have only five fingers on each hand. The solution is to use a special technique, based on sign language, which I call the Rule of “Thumb.” It is most effective for remembering three-digit and greater numbers. This technique not only is useful in this chapter but also will come in handy (pardon the pun) in subsequent chapters dealing with larger problems and longer numbers to remember.

You already know that to represent numbers 0 through 5, all you have to do is raise the equivalent number of fingers on your hand. When you get your thumb involved, it’s just as easy to represent numbers 6 through 9. Here are the Rules of “Thumb”:

• To hold on to 6, place your thumb on top of your pinky.

• To hold on to 7, place your thumb on top of your ring finger.

• To hold on to 8, place your thumb on top of your middle finger.

• To hold on to 9, place your thumb on top of your index finger.

With three-digit answers, hold the hundreds digit on your left hand and the tens digit on your right. When you get to the ones digit, you’ve reached the end of the problem (except for a possible remainder). Now say the number on your left hand, the number on your right hand, the one-digit you’ve just computed, and the remainder (in your head). Presto—you’ve said your answer!

For practice, try to compute the following four-digit division problem:

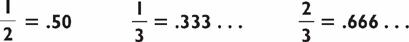
In using the Rule of “Thumb” to remember the answer, you’ll hold the 7 on your left hand by placing your thumb and ring finger together and the 6 on your right hand by placing your thumb and little finger together. Once you’ve calculated the ones digit (which is 3) and the remainder (which is 1), you can “read” the final answer off your hands from left to right: “seven … six … three with a remainder of one, or one-sixth.”

Some four-digit division problems yield four-digit answers. In that case, since you have only two hands, you will have to say the thousands digit of the answer out loud and use the rule of thumb to remember the rest of the answer. For example:

8352 ÷ 3

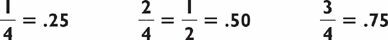
For this problem, you divide 3 into 8 to get your thousands digit of 2, say “two thousand” out loud, then divide 3 into 2352 in the usual way.

TWO-DIGIT DIVISION

This section assumes you already have mastered the art of dividing by a one-digit number. Naturally, division problems become harder as the number you divide by gets larger. Fortunately, I have some magic up my sleeve to make your life easier.

Let’s start with a relatively easy problem first:

597 ÷ 14

Since 597 lies between 14 × 10 and 14 × 100, the answer (also