Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

phonetic code to store the thousands digits (e.g., 447 = our rug) and put the hundreds digit (1) on my fingers:

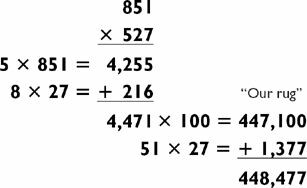
Let’s do another example, but this time I’ll break up the first number. (I usually break up the larger one so that the addition problem is easier.)

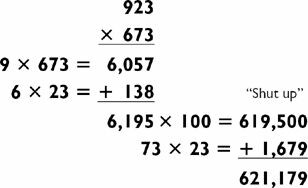
The following problems are embedded in the 5-by-5 multiplication problems in the next section:

5-BY-5 MULTIPLICATION

The largest problem we will attempt is the mental multiplication of two five-digit numbers. To do a 5-by-5, you need to have mastered 2-by-2s, 2-by-3s, and 3-by-3s, as well as the phonetic code. Now it is just a matter of putting it all together. As you did in the five-digit square problems, you will use the distributive law to break down the numbers. For example:

Based on this you can break down the problem into four easier multiplication problems, which I illustrate below in criss-cross fashion as a 2-by-2, two 3-by-2s, and finally a 3-by-3, summing the results for a grand total. That is,

(27 × 52) million
+ [(27 × 196) + (52 × 639)] thousand
+ (639 × 196)

As with the five-digit squares, I begin in the middle with the 3-by-2s, starting with the harder 3-by-2:

Committing 33,228 to memory with the mnemonic Mom, no knife, you then turn to the second 3-by-2:

2. 27 × 196 = 27 × (200 − 4) = 5,400 − 108 = 5,292

and add it to the number that you are storing:

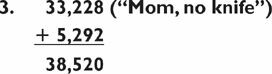
for a new total, which we store as:

“Movie lines” (38 million, 520 thousand)

Holding on to movie lines, compute the 2-by-2:

4. 52 × 27 = 52 × 9 × 3 = 1,404

At this point, you can give part of the answer. Since this 2-by-2 represents 52 × 27 million, 1,404 represents 1 billion, 404 million. Since 404 million will not cause a carry, you can safely say, “One billion …”

5. 404 + “Movie” (38) = 442

In this step you add 404 to movie (38) to get 442, at which point you can say, “… 442 million.…” You can say this because you know 442 will not carry—you’ve peeked ahead at the 3-by-3 to see whether it will cause 442 to carry to a higher number. If you found that it would carry, you would say, “443 million.” But since lines is 520,000 and the 3-by-3 (639 × 196) will not exceed 500,000 (a rough guesstimate of 600 × 200 = 120,000 shows this), you are safe.

6. 639 × 196 = 639 × 7 × 7 × 4 = 4,473 × 7 × 4 = 31,311 × 4 = 125,244

While still holding on to lines, you now compute the 3-by-3 using the factoring method, to get 125,244. You might convert 244 into a word like nearer. The final step is a simple addition of:

7. 125,244 + “Lines” (520,000)

This allows you to say the rest of the answer: “… 645,244.” Since a picture is worth a thousand calculations, here’s our picture of how this would look:

I should make a parenthetical note here that I am assuming in doing 5-by-5s that you can write down the problem on a blackboard or piece of paper. If you can’t, you will have to create a mnemonic for each of the four numbers. For example, in the last problem, you could store the problem as:

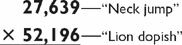
Then you would multiply lion × jump, dopish × neck, lion × neck, and finally dopish × jump. Obviously this would slow you down a bit, but if you want the extra challenge of not being able to see the numbers, you can still solve the problem.

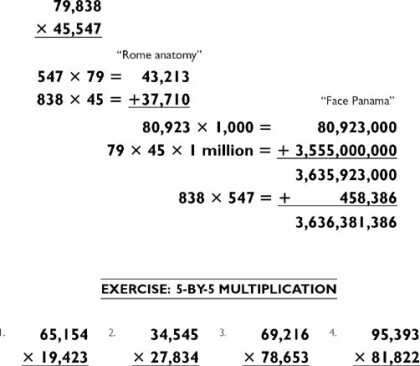
We conclude with one more 5-by-5 multiplication:

The steps are the same as those in the last problem. You start with the harder 3-by-2 and store the answer with a mnemonic:

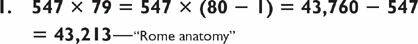
Then you compute the other 3-by-2.

2. 838 × 45 = 838 × 5 × 9 = 4,190 × 9 = 37,710

Summing the 3-by-2s you commit the new total to memory.

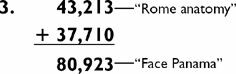
4. 79 × 45 = 79 × 9 × 5 = 711 × 5 = 3,555

The 2-by-2 gives you the first digit of the final answer, which you can say out loud with confidence: “Three billion …”

5. 555 + “Face” (80) = 635

The millions digits of the answer involve a carry from 635 to 636, because Panama (923) needs only 77,000 to cause it to carry, and the 3-by-3 (838 × 547) will easily exceed that figure. So you say: “… 636 million …”

The 3-by-3 is computed using the addition method:

And in the next step you add this total to Panama (923,000):

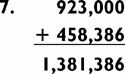
Since you’ve already used the 1 in the carry to 636 million, you just say the thousands: “… 381 thousand … 386,” and take a bow!

This problem may be illustrated in the following way:

Chapter 9 Presto-digit-ation: The Art of Mathematical Magic

Chapter 9

Presto-digit-ation: The Art of
Mathematical Magic

Playing with numbers has brought me great joy in life. I find that arithmetic can be just as entertaining as magic. But understanding the magical secrets of arithmetic requires algebra. Of course, there are other reasons to learn algebra (SATs, modeling real-world problems, computer programming, and understanding higher mathematics, to name just a few), but what first got me interested in algebra was the desire to understand some mathematical magic tricks, which I now present to you!

PSYCHIC MATH

Say to a volunteer in the audience, “Think of a number, any number.” And you should also say, “But to make it easy on yourself, think of a one-digit or two-digit number.” After you’ve reminded your volunteer that there’s no way you could know her number, ask her to:

1. double the number,

2. add 12,

3. divide the total by 2,

4. subtract the original number.

Then say, “Are you now thinking of the number six?” Try this one on yourself first and you will see that the sequence always produces the number 6 no matter what number is originally selected.

Why This Trick Works

This trick is based on simple algebra. In fact, I sometimes use this as a way to introduce algebra to students. The secret number that your volunteer chose can be represented by the letter x. Here are the functions you performed in the order you performed them:

1. 2x (double the number)

2. 2x + 12 (then add 12)

3. (2x + 12) ÷ 2 = × + 6 (then divide by 2)

4. x + 6 – x = 6 (then subtract original number)

So no matter what number your volunteer chooses, the final answer will always be 6. If you repeat this trick, have the volunteer add a different number at step 2 (say 18). The final answer will be half that number (namely 9).

THE MAGIC 1089!

Here is a trick that has been around for centuries. Have your audience member take out paper and pencil and:

1. secretly write down a three-digit number where the digits are decreasing (like 851 or 973),

2. reverse that number and subtract it from the first number,

3. take that answer and add it to the reverse of itself.

At the end of this sequence, the answer 1089 will magically appear, no matter what number your volunteer originally chose. For example:

Why This Trick Works

No matter what three-digit number you or anyone else chooses in this game, the final result will always be 1089. Why? Let abc denote the unknown three-digit number. Algebraically, this is equal to:

100a + 10b + c

When you reverse the number and subtract it from the original number, you get the number cba, algebraically equal to:

100c + 10b + a

Upon subtracting cba from abc, you get:

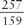
Hence, after subtracting in step 2, we must have one of the following multiples of 99: 198, 297, 396, 495, 594, 693, 792, or 891, each one of which will produce 1089 after adding it to the reverse of itself, as we did in step 3.

MISSING-DIGIT TRICKS

Using the number 1,089 from the last effect, hand a volunteer a calculator and ask her to multiply 1089 by any three-digit number she likes, but not to tell you the three-digit number. (Say she secretly multiplies 1,089 × 256 = 278,784.) Ask her how many digits are in her answer. She’ll reply, “Six.”

Next you say: “Call out five of your six digits to me in any order you like. I shall try to determine the missing digit.”

Suppose she calls out, “Two … four … seven … eight … eight.” You correctly tell her that she left out the number 7.

The secret is based on the fact that a number is a multiple of 9 if and only if its digits sum to a multiple of 9. Since 1 + 0 + 8 + 9 = 18 is a multiple of 9, then so is 1089. Thus 1089 times any whole number will also be a multiple of 9. Since the digits called out add up to 29, and the next multiple of 9 greater than 29 is 36, our volunteer must have left out the number 7 (since 29 + 7= 36).

There are more subtle ways to force the volunteer to end up with a multiple of 9. Here are some of my favorites:

1. Have the volunteer randomly choose a six-digit number, scramble its digits, then subtract the smaller six-digit number from the larger one. Since we’re subtracting two numbers with the same mod sum (indeed, the identical sum of digits), the resulting difference will have a mod sum of 0, and hence be a multiple of 9. Then continue as before to find the missing digit.

2. Have the volunteer secretly choose a four-digit number, reverse the digits, then subtract the smaller number from the larger. (This will be a multiple of 9.) Then multiply this by any three-digit number, and continue as before.

3. Ask the volunteer to multiply one-digit numbers randomly until the product is seven digits long. This is not “guaranteed” to produce a multiple of 9, but in practice it will do so at least 90% of the time (the chances are high that the one-digit numbers being multiplied include a 9 or two 3s or two 6s, or a 3 and a 6). I often use this method in front of mathematically advanced audiences who might see through other methods.

There is one problem to watch out for. Suppose the numbers called out add up to a multiple of 9 (say 18). Then you have no way of determining whether the missing digit is 0 or 9. How do you remedy that? Simple—you cheat! You merely say, “You didn’t leave out a zero, did you?” If she did leave out a 0, you have completed the trick successfully. If she did not leave out the 0, you say: “Oh, it seemed as though you were thinking of nothing! You didn’t leave out a one, two, three, or four, did you?” She’ll either shake her head, or say no. Then you follow with, “Nor did you leave out a five, six, seven, or eight, either. You left out the number nine, didn’t you?” She’ll respond in the affirmative, and you will receive your well-deserved applause!

LEAPFROG ADDITION

This trick combines a quick mental calculation with an astonishing prediction. Handing the spectator a card with ten lines, numbered 1 through 10, have the spectator think of two positive numbers between 1 and 20, and enter them on lines 1 and 2 of the card. Next have the spectator write the sum