Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

their weapons, their clothing, their tools, their trash? This is simply not how archaeology works.

5. Has anyone gone out of the way to disprove the claim, or has only confirmatory evidence been sought? This is the confirmation bias, or the tendency to seek confirmatory evidence and reject or ignore disconfirmatory evidence. The confirmation bias is powerful and pervasive and is almost impossible for any of us to avoid. It is why the methods of science that emphasize checking and rechecking, verification and replication, and especially attempts to falsify a claim are so critical.

6. Does the preponderance of evidence converge to the claimant’s conclusion, or a different one? The theory of evolution, for example, is proven through a convergence of evidence from a number of independent lines of inquiry. No one fossil, no one piece of biological or paleontological evidence has “evolution” written on it; instead there is a convergence of evidence from tens of thousands of evidentiary bits that adds up to a story of the evolution of life. Creationists conveniently ignore this convergence, focusing instead on trivial anomalies or currently unexplained phenomena in the history of life.

7. Is the claimant employing the accepted rules of reason and tools of research, or have these been abandoned in favor of others that lead to the desired conclusion? UFOlogists suffer this fallacy in their continued focus on a handful of unexplained atmospheric anomalies and visual misperceptions by eyewitnesses, while conveniently ignoring the fact that the vast majority (90 to 95 percent) of UFO sightings are fully explicable with prosaic answers.

8. Has the claimant provided a different explanation for the observed phenomena, or is it strictly a process of denying the existing explanation? This is a classic debate strategy—criticize your opponent and never affirm what you believe in order to avoid criticism. But this stratagem is unacceptable in science. Big Bang skeptics, for example, ignore the convergence of evidence of this cosmological model, focus on the few flaws in the accepted model, and have yet to offer a viable cosmological alternative that carries a preponderance of evidence in favor of it.

9. If the claimant has proffered a new explanation, does it account for as many phenomena as the old explanation? The HIV-AIDS skeptics argue that lifestyle, not HIV, causes AIDS. Yet, to make this argument they must ignore the convergence of evidence in support of HIV as the causal vector in AIDS, and simultaneously ignore such blatant evidence as the significant correlation between the rise in AIDS among hemophiliacs shortly after HIV was inadvertently introduced into the blood supply. On top of this, their alternative theory does not explain nearly as much of the data as the HIV theory.

10. Do the claimants’ personal beliefs and biases drive the conclusions, or vice versa? All scientists hold social, political, and ideological beliefs that could potentially slant their interpretations of the data, but how do those biases and beliefs affect their research? At some point, usually during the peer-review system, such biases and beliefs are rooted out, or the paper or book is rejected for publication. This is why one should not work in an intellectual vacuum. If you don’t catch the biases in your research, someone else will.

There is no definitive set of criteria we can apply in determining how open-minded we should be when encountering new claims and ideas, but with mathematical calculations on the odds of weird things happening and with an analysis of the sorts of questions we should ask when we encounter weird things, we have made a start toward coming to grips with our weird and wonderful world.

Answers

Answers

CHAPTER 1: A LITTLE GIVE AND TAKE

Two-Digit Addition (this page)

1. 23 + 16 = 23 + 10 + 6 = 33 + 6 = 39

2. 64 + 43 = 64 + 40 + 3 = 104 + 3 = 107

3. 95 + 32 = 95 + 30 + 2 = 125 + 2 = 127

4. 34 + 26 = 34 + 20 + 6 = 54 + 6 = 60

5. 89 + 78 = 89 + 70 + 8 = 159 + 8 = 167

6. 73 + 58 = 73 + 50 + 8 = 123 + 8 = 131

7. 47 + 36 = 47 + 30 + 6 = 77 + 6 = 83

8. 19 + 17 = 19 + 10 + 7= 29 + 7= 36

9. 55 + 49 = 55 + 40 + 9 = 95 + 9 = 104 10. 39 + 38 = 39 + 30 + 8 = 69 + 8 = 77

Three-Digit Addition (this page)

1. 242 + 137 = 242 + 100 + 30 + 7 = 342 + 30 + 7 = 372 + 7 = 379

2. 312 + 256 = 312 + 200 + 50 + 6 = 512 + 50 + 6 = 562 + 6 = 568

3. 635 + 814 = 635 + 800 + 10 + 4 = 1435 + 10 + 4 = 1445 + 4 = 1449

4. 457 + 241 = 457 + 200 + 40 + 1 = 657 + 40 + 1 = 697 + 1 = 698

5. 912 + 475 = 912 + 400 + 70 + 5 = 1312 + 70 + 5 = 1382 + 5 = 1387

6. 852 + 378 = 852 + 300 + 70 + 8 = 1 152 + 70 + 8 = 1222 + 8 = 1230

7. 457 + 269 = 457 + 200 + 60 + 9 = 657 + 60 + 9 = 717 + 9 = 726

8. 878 + 797 = 878 + 700 + 90 + 7 = 1578 + 90 + 7 = 1668 + 7 = 1675 or 878 + 797 = 878 + 800 − 3 = 1678 − 3 = 1675

9. 276 + 689 = 276 + 600 + 80 + 9 = 876 + 80 + 9 = 956 + 9 = 965

10. 877 + 539 = 877 + 500 + 30 + 9 = 1 377 + 30 + 9 = 1407 + 9 = 1416

11. 5400 + 252 = 5400 + 200 + 52 = 5600 + 52 = 5652

12. 1800 + 855 = 1800 + 800 + 55 = 2600 + 55 = 2655

13. 6120 + 136 = 6120 + 100 + 30 + 6 = 6220 + 30 + 6 = 6250 + 6 = 6256

14. 7830 + 348 = 7830 + 300 + 40 + 8 = 81 30 + 40 + 8 = 8170 + 8 = 8178

15. 4240 + 371 = 4240 + 300 + 70 + 1 = 4540 + 70 + 1 = 4610 + 1 = 4611

Two-Digit Subtraction (this page)

1. 38 − 23 = 38 − 20 − 3 = 18 − 3 = 15

2. 84 − 59 = 84 − 60 + 1 = 24 + 1 =25

3. 92 − 34 = 92 − 40 + 6 = 52 + 6 = 58

4. 67 − 48 = 67 − 50 + 2 = 17 + 2 = 19

5. 79 − 29 = 79 − 20 − 9 = 59 − 9 = 50 or 79 − 29 = 79 − 30 + 1 = 49 + 1 = 50

6. 63 – 46 = 63 − 50 + 4 = 13 + 4 = 17

7. 51 – 27 = 51 − 30 + 3 = 21 + 3 = 24

8. 89 − 48 = 89 − 40 − 8 = 49 − 8 = 41

9. 125 − 79 = 125 − 80 + 1 = 45 + 1 = 46

10. 148 − 86 = 148 − 90 + 4 = 58 + 4 = 62

Three-Digit Subtraction (this page)

1. 583 − 271 = 583 − 200 − 70 − 1 = 383 − 70 − 1 = 313 − 1 = 312

2. 936 − 725 = 936 − 700 − 20 − 5 = 236 − 20 − 5 = 216 − 5 = 211

3. 587 − 298 = 587 − 300 + 2 = 287 + 2 = 289

4. 763 − 486 = 763 − 500 + 14 = 263 + 14 = 277

5. 204 − 185 = 204 − 200 + 15 = 04 + 15 = 19

6. 793 − 402 = 793 − 400 − 2 = 393 − 2 = 391

7. 219 − 176 = 219 − 200 + 24 = 19 + 24 = 43

8. 978 − 784 = 978 − 800 + 16 = 178 + 16 = 194

9. 455 − 319 = 455 − 400 + 81 = 55 + 81 = 136

10. 772 − 596 = 772 − 600 + 4 = 172 + 4 = 176

11. 873 − 357 = 873 − 400 + 43 = 473 + 43 = 516

12. 564 − 228 = 564 − 300 + 72 = 264 + 72 = 336

13. 1428 − 571 = 1428 − 600 + 29 = 828 + 29 = 857

14. 2345 − 678 = 2345 − 700 + 22 = 1645 + 22 = 1667

15. 1776 − 987 = 1776 − 1000 + 13 = 776 + 13 = 789

CHAPTER 2: PRODUCTS OF A MISSPENT YOUTH

2-by-1 Multiplication (this page)

3-by-1 Multiplication (this page)

Two-Digit Squares (this page)

CHAPTER 3: NEW AND IMPROVED PRODUCTS

Multiplying by 11 (this page)

2-by-2 Addition-Method Multiplication Problems (this page)

2-by-2 Subtraction-Method Multiplication Problems (this page)

2-by-2 Factoring-Method Multiplication Problems (this page)

1. 27 × 14 = 27 × 7 × 2 = 189 × 2 = 378 or 14 × 27 = 14 × 9 × 3 = 126 × 3 = 378

2. 86 × 28 = 86 × 7 × 4 = 602 × 4 = 2408

3. 57 × 14 = 57 × 7 × 2 = 399 × 2 = 798

4. 81 × 48 = 81 × 8 × 6 = 648 × 6 = 3888 or 48 × 81 = 48 × 9 × 9 = 432 × 9 = 3888

5. 56 × 29 = 29 × 7 × 8 = 203 × 8 = 1624

6. 83 × 18 = 83 × 6 × 3 = 498 × 3 = 1494

7. 72 × 17 = 17 × 9 × 8 = 153 × 8 = 1224

8. 85 × 42 = 85 × 6 × 7 = 510 × 7 = 3570

9. 33 × 16 = 33 × 8 × 2 = 264 × 2 = 528 or 16 × 33 = 16 × 11 × 3 = 176 × 3 = 528

10. 62 × 77 = 62 × 11 × 7 = 682 × 7 = 4774

11. 45 × 36 = 45 × 6 × 6 = 270 × 6 = 1620 or 45 × 36 = 45 × 9 × 4 = 405 × 4 = 1620 or 36 × 45 = 36 × 9 × 5 = 324 × 5 = 1620 or 36 × 45 = 36 × 5 × 9 = 180 × 9 = 1620

12. 37 × 48 = 37 × 8 × 6 = 296 × 6 = 1776

2-by-2 General Multiplication—Anything Goes! (this page)

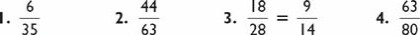
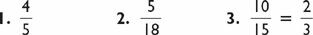
Three-Digit Squares (this page)

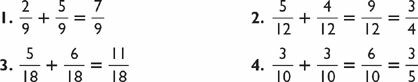
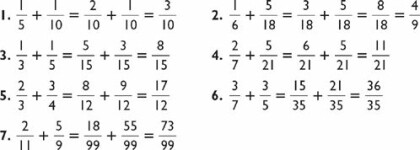
Two-Digit Cubes (this page)

1. 123 = (10 × 12 × 14) + (22