Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

order to do these problems, it is particularly important that you are comfortable and reasonably fast using the phonetic code. And even though, if you glance ahead in this chapter, the problems seem overwhelming, let me restate the two fundamental premises of this book: (1) all mental calculation skills can be learned by almost anyone; and (2) the key is the simplification of all problems into easier problems that can be done quickly. There is no problem in this chapter (or anywhere else) that you will encounter (comparable to these) that cannot be mastered and learned through the simplification techniques you’ve learned in previous chapters. Because we are assuming that you’ve mastered the techniques needed for this chapter, we will be teaching primarily by illustration, rather than walking you through the problems word for word. As an aid, however, we remind you that many of the simpler problems embedded within these larger problems are ones you have already encountered in previous chapters. We begin with four-digit squares. Good luck!

FOUR-DIGIT SQUARES

As a preliminary skill for mastering four-digit squares, you need to be able to do 4-by-1 problems. We break these down into two 2-by-1 problems, as in the examples below:

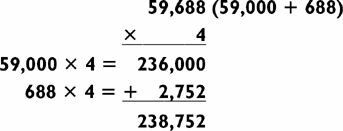
Once you’ve mastered 4-by-1s you’re ready to tackle four-digit squares. Let’s square 4,267. Using the same method we used with two-digit and three-digit squares, we’ll square the number 4,267 by rounding down by 267 to 4,000, and up by 267 to 4,534, multiplying 4,534 × 4,000 (a 4-by-1), and then adding the square of the number you went up and down by, or 2672, as illustrated below:

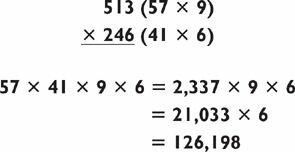
Now, obviously there is a lot going on in this problem. I realize it’s one thing to say, “Just add the square of 267” and quite another to actually do it and remember what it was you were supposed to add to it. First of all, once you multiply 4,534 × 4 to get 18,136, you can actually say the first part of the answer out loud: “Eighteen million …” You can do so because the original number is always rounded to the nearest thousand. Thus the largest three-digit number you will ever square in the next step is 500. The square of 500 is 250,000, so as soon as you see that the rest of your answer (in this case, 136,000) is less than 750,000, you know that the millions digit will not change.

Once you’ve said “eighteen million …,” you need to hold on to 136,000 before you square 267. Here’s where our mnemonics from the last chapter comes to the rescue! Using the phonetic code, you can convert 136 to damage (1 = d, 3 = m, 6 = j). Now you can work on the next part of the problem and just remember damage (and that there are three zeros following—this will always be the case). If at any time in the computations you forget what the original problem is, you can either glance at the original number or, if it isn’t written down, ask the audience to repeat the problem (which gives the illusion you are starting the problem over from scratch when, in fact, you have already done some of the calculations)!

You now do the three-digit square just as you learned to do before, to get 71,289. I used to have trouble remembering the hundreds digits of my answer (2, in this case). I cured this by raising my fingers (two fingers here). If you forget the last two digits (89), you can go back to the original number (4,267), square its last two digits (672 = 4,489), and take the last two digits of that.

To compute the final answer, you now add 71,289 to damage (which translates back to 136,000) resulting in 207,289, which you may now say out loud.

Let’s do one more four-digit square—8,4312:

Without repeating all the detailed steps as we did in the last problem, I will point out some of the highlights of this problem. After doing the 8 × 8,862 = 70,896, note that 896 is above 750, so a carry is possible. In fact, since 4312 is greater than 4002 = 160,000, there definitely will be a carry when you do the addition to the number 896,000. Hence we can safely say aloud, “Seventy-one million …” at this point.

When you square 431, you get 185,761. Add the 185 to the 896 to get 1,081, and say the rest of the answer. But remember that you already anticipated the carry, so you just say, “… 81 thousand … 761.” You’re done!

We illustrate one more fine point with 2,7532:

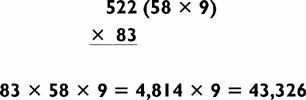
Since you are rounding up to 3,000, you will be multiplying 3,000 by another number in the 2,000s. You could subtract 2,753 − 247 = 2,506, but that’s a little messy. To obtain the last three digits, double 753 to get 1,506. The last three digits of this number, 506, are the last three digits of the 2,000 number: 2,506! This works because the two numbers being multiplied must add to twice the original number.

Then proceed in the usual manner of multiplying 3,000 × 2,506 = 7,518,000, convert 518 to the words light off, and say the first part of the answer out loud as “Seven million …” You can say this with confidence since 518 is below 750, so there will not be a carry.

Thomas Fuller: Learned Men and Great Fools

It would be hard to top the physical handicap on learning experienced by Helen Keller, though the social handicap imposed on Thomas Fuller, born in Africa in 1710, comes close. He was not only illiterate; he was forced to work in the fields of Virginia as a slave and never received a single day of education. The “property” of Mrs. Elizabeth Cox, Thomas Fuller taught himself to count to 100, after which he increased his numerical powers by counting such items at hand as the grains in a bushel of wheat, the seeds in a bushel of flax, and the number of hairs in a cow’s tail (2,872).

Extrapolating from mere counting, Fuller learned to compute the number of shingles a house would need to cover its roof, the number of posts needed to enclose it, and other numbers relevant to materials needed in construction. His prodigious skills grew, and with them his reputation. In his old age, two Pennsylvanians challenged him to compute, in his head, numbers that would challenge the best lightning calculators. For example, they asked: “Suppose a farmer has six sows, and each sow has six female pigs the first year, and they all increase in the same proportion, to the end of eight years, how many sows will the farmer then have?” The problem can be written as 78 × 6, that is, (7 × 7 × 7 × 7 × 7 × 7 × 7 × 7)X 6. Within ten minutes Fuller gave his response of 34,588,806, the correct answer.

Upon Fuller’s death in 1790, the Columbian Centinel reported that “he could give the number of poles, yards, feet, inches, and barleycorns in any given distance, say the diameter of the earth’s orbit; and in every calculation he would produce the true answer, in less time than ninety-nine men in a hundred would take with their pens.” When Fuller was asked if he regretted having never gained a traditional education he responded: “No, Massa—it is best I got no learning: for many learned men be great fools.”

Next, you add the square of 247. Don’t forget that you can derive 247 quickly as the complement of 753. Then proceed to the final answer as you did in the previous four-digit problems.

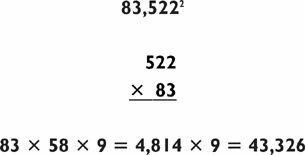
3-BY-2 MULTIPLICATION

We saw in the 2-by-2 multiplication problems that there are several different ways to tackle the same problem. The variety of methods increases when you increase the number of digits in the problem. In 3-by-2 multiplication I find that it pays to take a few moments to look at the problem to determine the method of calculation that will put the least amount of strain on the brain.

Factoring Methods

The easiest 3-by-2 problems to compute are those in which the two-digit number is factorable.

For example:

These are great because you don’t have to add anything. You just factor 56 into 8 × 7, then do a 3-by-1 (637 × 8 = 5,096), and finally a 4-by-1 (5,096 × 7 = 35,672). There are no addition steps and you don’t have to store any partial results.

More than half of all two-digit numbers are factorable into numbers 11 and below, so you’ll be able to use this method for many problems. Here’s an example:

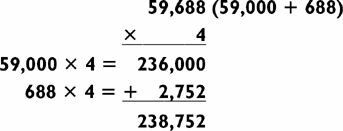
To multiply 853 × 11, you treat 853 as 850 + 3 and proceed as follows:

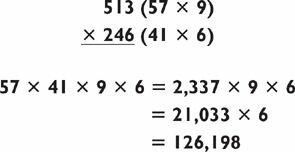
Now multiply 9,383 × 4 by treating 9,383 as 9,300 + 83, as follows:

If the two-digit number is not factorable into small numbers, examine the three-digit number to see if it can be factored:

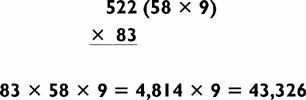
Notice that the sequence of the multiplication problems is a 2-by-1, a 3-by-1, and finally a 4-by-1. Since these are all problems you can now do with considerable ease, this type of 3-by-2 problem should be no problem at all.

Here’s another example where the two-digit number is not factorable but the three-digit number is:

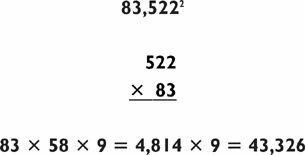
Here the sequence is a 2-by-2, a 3-by-1, and a 4-by-1, though when the three-digit number is factorable by 11, you can use the elevens method for a very simple 2-by-2 (53 × 11 = 583). In this case it pays to be able to recognize when a number is divisible by 11, as described in Chapter 4.

If the two-digit number is not factorable, and the three-digit number is factorable into only a 2-by-1, the problem can still be handled easily by a 2-by-2, followed by a 4-by-1:

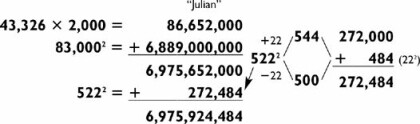
Here you need to see that 423 is divisible by 9, setting up the problem as 83 × 47 × 9. This 2-by-2 is not so easy, but by treating 83 as 80 + 3, you get:

Then do the 4-by-1 problem of 3,901 × 9 for your final answer of 35,109.

The Addition Method

If the two-digit number and the three-digit number cannot be conveniently factored in the 3-by-2 problem you’re doing, you can always resort to the addition method:

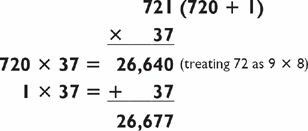
The method requires you to add a 2-by-2 (times 10) to a 2-by-1. These problems tend to be more difficult than problems that can be factored since you have to perform a 2-by-1 while holding on to a five-digit number, and then add the results together. In fact, it is probably easier to solve this problem by factoring 721 into 103 × 7, then computing 37 × 103 × 7 = 3,811 × 7 = 26,677.

Here’s another example:

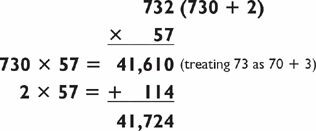
Though you will usually break up the three-digit number when using the addition method, it occasionally pays to break up the two-digit number instead, particularly when the last digit of the two-digit number is a 1 or a 2, as in the following example:

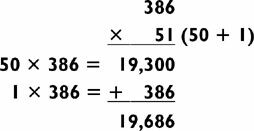
This reduces the 3-by-2 to a 3-by-1, made especially easy since the second multiplication problem involves a 1. Note, too, that we were aided in multiplying a 5 by an even number, which produces an extra 0 in the answer, so there is only one digit of overlap in the addition problem.

Another example of multiplying a 5 by an even number is illustrated in the following problem:

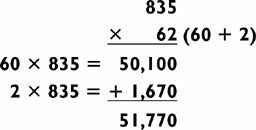
When you multiply the 6 in 60 by the 5 in 835, it generates an extra 0 in the answer, making the addition problem especially easy.

The Subtraction Method

As with 2-by-2s, it is sometimes more convenient to solve a 3-by-2 with subtraction instead of addition, as in the following problems:

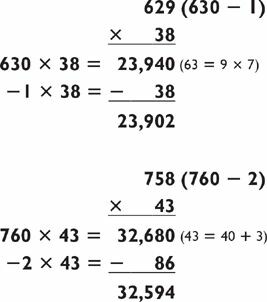
By contrast, you can compare the last subtraction method with the addition method, below, for this same problem:

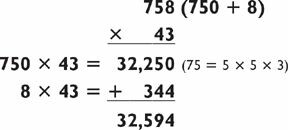
My preference for tackling this problem would be to use the subtraction method because I always try to leave myself with the easiest possible addition or subtraction problem at the end. In this case, I’d rather subtract 86 than add 344, even though the 2-by-2