Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

- Author: Arthur Benjamin
Book online «Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗». Author Arthur Benjamin
Chapter 6
Math for the Board:
Pencil-and-Paper Math
In the Introduction to this book I discussed the many benefits you will get from being able to do mental calculations. In this chapter I present some methods for speeding up pencil-and-paper calculations as well. Since calculators have replaced much of the need for pencil-and-paper arithmetic in most practical situations, I’ve chosen to concentrate on the lost art of calculating square roots and the flashy criss-cross method for multiplying large numbers. Since these are, admittedly, mostly for mental gymnastics and not for some practical application, I will first touch on addition and subtraction and show you just a couple of little tricks for speeding up the process and for checking your answers. These techniques can be used in daily life, as you’ll see.
If you are eager to get to the more challenging multiplication problems, you can skip this chapter and go directly to Chapter 7, which is critical for mastering the big problems in Chapter 8. If you need a break and just want to have some fun, then I recommend going through this chapter—you’ll enjoy playing with pencil and paper once again.
COLUMNS OF NUMBERS
Adding long columns of numbers is just the sort of problem you might run into in business or while figuring out your personal finances. Add the following column of numbers as you normally would and then check to see how I do it.
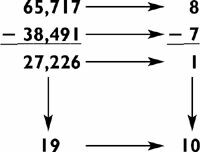
When I have pencil and paper at my disposal, I add the numbers from top to bottom and from right to left, just as we learned to do in school. With practice, you can do these problems in your head as fast or faster than you can with a calculator. As I sum the digits, the only numbers that I “hear” are the partial sums. That is, when I sum the first (rightmost) column 8 + 4 + 0 + 7 + 7 + 5, I hear 8 … 12 … 19 … 26 … 31. Then I put down the 1, carry the 3, and proceed as usual. The next column would then sound like 3 … 5 … 13 … 15 … 22 … 23 … 25. Once I have my final answer, I write it down, then check my computation by adding the numbers from bottom to top and, I hope, arrive at the same answer.
For instance, the first column would be summed, from bottom to top, as 5 + 7 + 7 + 0 + 4 + 8 (which in my mind sounds like 5 … 12 … 19 … 23 … 31). Then I mentally carry the 3, and add 3 + 2 + 1 + 7 + 2 + 8 + 2, and so on. By adding the numbers in a different order, you are less likely to make the same mistake twice. Of course, if the answers differ, then at least one of the calculations must be wrong.
MOD SUMS
If I’m not sure about my answer, I sometimes check my solution by a method I call mod sums (because it is based on the elegant mathematics of modular arithmetic). This method also goes by the names of digital roots and casting out nines. I admit this method is not as practical, but it’s easy to use.
With the mod sums method, you sum the digits of each number until you are left with a single digit. For example, to compute the mod sum of 4328, add 4 + 3 + 2 + 8 = 17. Then add the digits of 17 to get 1 + 7 = 8. Hence the mod sum of 4328 is 8. For the previous problem the mod sums of each number are computed as follows:

As illustrated above, the next step is to add all the mod sums together (8 + 2 + 8 + 1 + 5 + 5). This yields 29, which sums to 11, which in turn sums to 2. Note that the mod sum of 8651, your original total of the original digits, is also 2. This is not a coincidence! If you have computed the answer and the mod sums correctly, your final mod sums must be the same. If they are different, you have definitely made a mistake somewhere: there is about a 1 in 9 chance that the mod sums will match accidentally. If there is a mistake, then this method will detect it 8 times out of 9.
The mod sum method is more commonly known to mathematicians and accountants as casting out nines because the mod sum of a number happens to be equal to the remainder obtained when the number is divided by 9. In the case of the answer above—8651—the mod sum was 2. If you divide 8651 by 9, the answer is 961 with a remainder of 2. In other words, if you cast out 9 from 8651 a total of 961 times, you’ll have a remainder of 2. There’s one small exception to this. Recall that the sum of the digits of any multiple of 9 is also a multiple of 9. Thus, if a number is a multiple of 9, it will have a mod sum of 9, even though it has a remainder of 0.
SUBTRACTING ON PAPER
You can’t, of course, subtract columns of numbers the same way you add them. Rather, you subtract them number by number, which means that all subtraction problems involve just two numbers. Once again, with pencil and paper at our disposal, it is easier to subtract from right to left. To check your answer, just add the answer to the second number. If you are correct, then you should get the top number.
If you want, you can also use mod sums to check your answer. The key is to subtract the mod sums you arrive at and then compare that number to the mod sum of your answer:

There’s one extra twist. If the difference in the mod sums is a negative number or 0, add 9 to it. For instance:
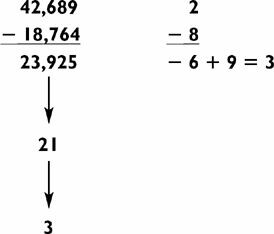
PENCIL-AND-PAPER SQUARE ROOTS
With the advent of pocket calculators, the pencil-and-paper method of calculating square roots has practically become a lost art. You’ve already seen how to estimate square roots mentally. Now I’ll show you how to do it exactly, using pencil and paper.
Remember how in guesstimating square roots you calculated the square root of nineteen? Let’s look at that problem again, this time using a method that will give you the exact square root.
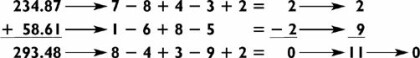
I will describe the general method that fits all cases, and illustrate it with the above example.
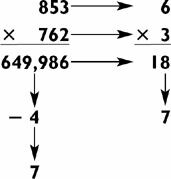
Step 1. If the number of digits to the left of the decimal point is one, three, five, seven, or any odd number of digits, the first digit of the answer (or quotient) will be the largest number whose square is less than the first digit of the original number. If the number of digits to the left of the decimal point is two, four, six, or any even number of digits, the first digit of the quotient will be the largest number whose square is less than the first two digits of the dividend. In this case, 19 is a two-digit number, so the first digit of the quotient is the largest number whose square is less than 19. That number is 4. Write the answer above either the first digit of the dividend (if odd) or the second digit of the dividend (if even).
Step 2. Subtract the square of the number in step 1, then bring down two more digits. Since 42 = 16, we subtract 19 − 16 = 3. We bring down two 0s, leaving 300 as the current remainder.
Step 3. Double the current quotient (ignoring any decimal point), and put a blank space in following it. Here 4 × 2 = 8. Put down 8_ x_ to the left of the current remainder, in this case 300.
Step 4. The next digit of the quotient will be the largest number that can be put in both blanks so that the resulting multiplication problem is less than or equal to the current remainder. In this case the number is 3, because 83 × 3 = 249, whereas 84 × 4 = 336, which is too high. Write this number above the second digit of the next two numbers; in this case the 3 would go above the second 0. We now have a quotient of 4.3.
Step 5. If you want more digits, subtract the product from the remainder (i.e., 300 − 249 = 51), and bring down the next two digits; in this case 51 turns into 5100, which becomes the current remainder. Now repeat steps 3 and 4.
To get the third digit of the square root, double the quotient, again ignoring the decimal point (i.e., 43 × 2 = 86). Place 86_ x_ to the left of 5100. The number 5 gives us 865 × 5 = 4325, the largest product below 5100. The 5 goes above the next two numbers, in this case two more 0s. We now have a quotient of 4.35. For even more digits, repeat the process as we’ve done in the example.
Here’s an example of an odd number of digits before the decimal point:
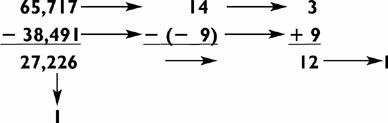
Next, we’ll calculate the square root of a four-digit number. In this case—as with two-digit numbers—we consider the first two digits of the problem to determine the first digit of the square root:
Finally, if the number for which you are calculating the square root is a perfect square, you will know it as soon as you end up with a remainder of 0 and nothing to bring down. For example:
PENCIL-AND-PAPER MULTIPLICATION
For pencil-and-paper multiplication I use the criss-cross method, which enables me to write down the entire answer on one line without ever writing any partial results! This is one of the most impressive displays of mathemagics when you have pencil and paper at your disposal. Many lightning calculators in the past earned their reputations with this method. They would be given two large numbers and write down the answer almost instantaneously. The criss-cross method is best learned by example.
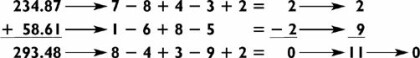
Step 1. First, multiply 4 × 7 to yield 28, write down the 8, and mentally carry the 2 to the next computation, below.
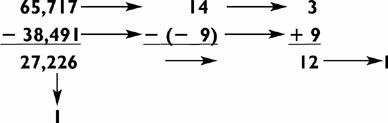
Step 2. Following the diagram, add 2 + (4 × 4) + (3 × 7) = 39, write down the 9, and carry the 3 to the final computation, below.

Step 3. End by adding 3 + (3 × 4) = 15 and writing down 15 to arrive at your final answer.
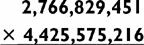
You have now written the answer: 1598.
Let’s solve another 2-by-2 multiplication problem using the criss-cross method:

The steps and diagrams appear as follows:
Step 1. 5 × 3 = 15

Step 2. 1 + (5 × 8) + (6 × 3) = 59

Step 3. 5 + (6 × 8) = 53

Answer: 5395
The criss-cross method gets slightly more complicated with 3-by-3 problems.

We proceed as suggested by our pattern below:
Step 1. 2 × 3 = 6

Step 2. (2 × 5) + (6 × 3) = 28

Step 3. 2 + (2 × 8) + (7 × 3) + (6 × 5) = 69
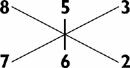
Step 4. 6 + (6 × 8) + (7 ×




Comments (0)