Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

our 800 hotline. Art and I are both credentialed in the most conservative of academic professions—Art in mathematics and I, myself, in the history of science—and we would never risk career embarrassment (or worse) by making such powerful claims if they were not true. To put it simply, this stuff works, and virtually everyone can do it because this art of “math genius” is a learned skill. So you can look forward to improving your math skills, impressing your friends, enhancing your memory, and, most of all, having fun! Introduction by Arthur Benjamin

Introduction

Ever since I was a child, I have loved playing with numbers, and in this book I hope to share my passion with you. I have always found numbers to have a certain magical appeal and spent countless hours entertaining myself and others with their beautiful properties. As a teenager, I performed as a magician, and subsequently combined my loves of math and magic into a full-length show, called Mathemagics, where I would demonstrate and explain the secrets of rapid mental calculation to audiences of all ages.

Since earning my PhD, I have taught mathematics at Harvey Mudd College, and I still enjoy sharing the joy of numbers with children and adults throughout the world. In this book, I will share all of my secrets for doing math in your head, quickly and easily. (I realize that magicians are not supposed to reveal their secrets, but mathemagicians have a different code of ethics. Mathematics should be awe inspiring, not mysterious.)

What will you learn from this book? You will learn to do math in your head faster than you ever thought possible. After a little practice, you will dramatically improve your memory for numbers. You will learn feats of mind that will impress your friends, colleagues, and teachers. But you will also learn to view math as an activity that can actually be fun.

Too often, math is taught as a set of rigid rules, leaving little room for creative thinking. But as you will learn from Secrets, there are often several ways to solve the same problem. Large problems can be broken down into smaller, more manageable components. We look for special features to make our problems easier to solve. These strike me as being valuable life lessons that we can use in approaching all kinds of problems, mathematical and otherwise.

“But isn’t math talent something that you are born with?” I get this question all the time. Many people are convinced that lightning calculators are prodigiously gifted. Maybe I was born with some curiosity about how things work, whether it be a math problem or a magic trick. But I am convinced, based on many years of teaching experience, that rapid math is a skill that anyone can learn. And like any worthwhile skill, it takes practice and dedication if you wish to become an expert. But to achieve these results efficiently, it is important that you practice the right way. Let me show you the way!

Mathemagically,

Dr. Arthur Benjamin

Claremont, California

Chapter 0 Quick Tricks: Easy (and Impressive) Calculations

Chapter 0

Quick Tricks:
Easy (and Impressive) Calculations

In the pages that follow, you will learn to do math in your head faster than you ever thought possible. After practicing the methods in this book for just a little while, your ability to work with numbers will increase dramatically. With even more practice, you will be able to perform many calculations faster than someone using a calculator. But in this chapter, my goal is to teach you some easy yet impressive calculations you can learn to do immediately. We’ll save some of the more serious stuff for later.

INSTANT MULTIPLICATION

Let’s begin with one of my favorite feats of mental math—how to multiply, in your head, any two-digit number by eleven. It’s very easy once you know the secret. Consider the problem:

32×11

To solve this problem, simply add the digits, 3 + 2 = 5, put the 5 between the 3 and the 2, and there is your answer:

352

What could be easier? Now you try:

53 × 11

Since 5 + 3 = 8, your answer is simply

583

One more. Without looking at the answer or writing anything down, what is

81×11?

Did you get 891? Congratulations!

Now before you get too excited, I have shown you only half of what you need to know. Suppose the problem is

85 × 11

Although 8 + 5 = 13, the answer is NOT 8135!

As before, the 3 goes in between the numbers, but the 1 needs to be added to the 8 to get the correct answer:

935

Think of the problem this way:

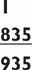
Here is another example. Try 57 × 11.

Since 5 + 7 = 12, the answer is

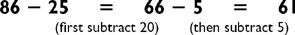
Okay, now it’s your turn. As fast as you can, what is

77 × 11?

If you got the answer 847, then give yourself a pat on the back. You are on your way to becoming a mathemagician.

Now, I know from experience that if you tell a friend or teacher that you can multiply, in your head, any two-digit number by eleven, it won’t be long before they ask you to do 99 × 11. Let’s do that one now, so we are ready for it.

Since 9 + 9 = 18, the answer is:

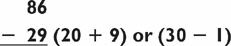
Okay, take a moment to practice your new skill a few times, then start showing off. You will be amazed at the reaction you get. (Whether or not you decide to reveal the secret is up to you!)

Welcome back. At this point, you probably have a few questions, such as:

“Can we use this method for multiplying three-digit numbers (or larger) by eleven?”

Absolutely. For instance, for the problem 314 × 11, the answer still begins with 3 and ends with 4. Since 3 + 1 = 4, and 1 + 4 = 5, the answer is 3454. But we’ll save larger problems like this for later.

More practically, you are probably saying to yourself,

“Well, this is fine for multiplying by elevens, but what about larger numbers? How do I multiply numbers by twelve, or thirteen, or thirty-six?”

My answer to that is, Patience! That’s what the rest of the book is all about. In Chapters 2, 3, 6, and 8, you will learn methods for multiplying together just about any two numbers. Better still, you don’t have to memorize special rules for every number. Just a handful of techniques is all that it takes to multiply numbers in your head, quickly and easily.

SQUARING AND MORE

Here is another quick trick.

As you probably know, the square of a number is a number multiplied by itself. For example, the square of 7 is 7 × 7 = 49. Later, I will teach you a simple method that will enable you to easily calculate the square of any two-digit or three-digit (or higher) number. That method is especially simple when the number ends in 5, so let’s do that trick now.

To square a two-digit number that ends in 5, you need to remember only two things.

1. The answer begins by multiplying the first digit by the next higher digit.

2. The answer ends in 25.

For example, to square the number 35, we simply multiply the first digit (3) by the next higher digit (4), then attach 25. Since 3 × 4 = 12, the answer is 1225. Therefore, 35 × 35 = 1225. Our steps can be illustrated this way:

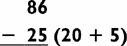
How about the square of 85? Since 8 × 9 = 72, we immediately get 85 × 85 = 7225.

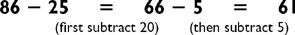
We can use a similar trick when multiplying two-digit numbers with the same first digit, and second digits that sum to 10. The answer begins the same way that it did before (the first digit multiplied by the next higher digit), followed by the product of the second digits. For example, let’s try 83 × 87. (Both numbers begin with 8, and the last digits sum to 3 + 7 = 10.) Since 8 × 9 = 72, and 3 × 7 = 21, the answer is 7221.

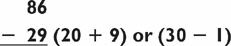
Similarly, 84 × 86 = 7224.

Now it’s your turn. Try

26 × 24

How does the answer begin? With 2 × 3 = 6. How does it end? With 6 × 4 = 24. Thus 26 × 24 = 624.

Remember that to use this method, the first digits have to be the same, and the last digits must sum to 10. Thus, we can use this method to instantly determine that

31 × 39 = 1209
32 × 38 = 1216
33 × 37 = 1221
34 × 36 = 1224
35 × 35 = 1225

You may ask,

“What if the last digits do not sum to ten? Can we use this method to multiply twenty-two and twenty-three?”

Well, not yet. But in Chapter 8, I will show you an easy way to do problems like this using the close-together method. (For 22 × 23, you would do 20 × 25 plus 2 × 3, to get 500 + 6 = 506, but I’m getting ahead of myself!) Not only will you learn how to use these methods, but you will understand why these methods work, too.

“Are there any tricks for doing mental addition and subtraction?”

Definitely, and that is what the next chapter is all about. If I were forced to summarize my method in three words, I would say, “Left to right.” Here is a sneak preview.

Consider the subtraction problem

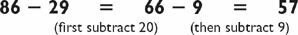
Most people would not like to do this problem in their head (or even on paper!), but let’s simplify it. Instead of subtracting 587, subtract 600. Since 1200 − 600 = 600, we have that

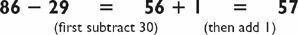
But we have subtracted 13 too much. (We will explain how to quickly determine the 13 in Chapter 1.) Thus, our painful-looking subtraction problem becomes the easy addition problem

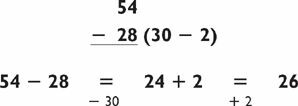
which is not too hard to calculate in your head (especially from left to right). Thus, 1241 − 587 = 654.

Using a little bit of mathematical magic, described in Chapter 9, you will be able to instantly compute the sum of the ten numbers below.

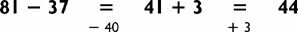
Although I won’t reveal the magical secret right now, here is a hint. The answer, 935, has appeared elsewhere in this chapter. More tricks for doing math on paper will be found in Chapter 6. Furthermore, you will be able to quickly give the quotient of the last two numbers:

359 ÷ 222 = 1.61 (first three digits)

We will have much more to say about division (including decimals and fractions) in Chapter 4.

MORE PRACTICAL TIPS

Here’s a quick tip for calculating tips. Suppose your bill at a restaurant came to $42, and you wanted to leave a 15% tip. First we