Secrets of Mental Math, Arthur Benjamin [management books to read .txt] 📗

calculate 10% of $42, which is $4.20. If we cut that number in half, we get $2.10, which is 5% of the bill. Adding these numbers together gives us $6.30, which is exactly 15% of the bill. We will discuss strategies for calculating sales tax, discounts, compound interest, and other practical items in Chapter 5, along with strategies that you can use for quick mental estimation when an exact answer is not required.

IMPROVE YOUR MEMORY

In Chapter 7, you will learn a useful technique for memorizing numbers. This will be handy in and out of the classroom. Using an easy-to-learn system for turning numbers into words, you will be able to quickly and easily memorize any numbers: dates, phone numbers, whatever you want.

Speaking of dates, how would you like to be able to figure out the day of the week of any date? You can use this to figure out birth dates, historical dates, future appointments, and so on. I will show you this in more detail later, but here is a simple way to figure out the day of January 1 for any year in the twenty-first century. First familiarize yourself with the following table.

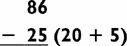
For instance, let’s determine the day of the week of January 1, 2030. Take the last two digits of the year, and consider it to be your bill at a restaurant. (In this case, your bill would be $30.) Now add a 25% tip, but keep the change. (You can compute this by cutting the bill in half twice, and ignoring any change. Half of $30 is $15. Then half of $15 is $7.50. Keeping the change results in a $7 tip.) Hence your bill plus tip amounts to $37. To figure out the day of the week, subtract the biggest multiple of 7 (0, 7, 14, 21, 28, 35, 42, 49, …) from your total, and that will tell you the day of the week. In this case, 37 − 35 = 2, and so January 1, 2030, will occur on 2’s day, namely Tuesday:

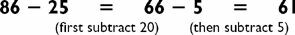
How about January 1, 2043:

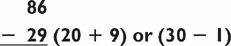
Exception: If the year is a leap year, remove $1 from your tip, then proceed as before. For example, for January 1, 2032, a 25% tip of $32 would be $8. Removing one dollar gives a total of 32 + 7 = 39. Subtracting the largest multiple of 7 gives us 39 − 35 = 4. So January 1, 2032, will be on 4’s day, namely Thursday. For more details that will allow you to compute the day of the week of any date in history, see Chapter 9. (In fact, it’s perfectly okay to read that chapter first!)

I know what you are wondering now:

“Why didn’t they teach this to us in school?”

I’m afraid that there are some questions that even I cannot answer. Are you ready to learn more magical math? Well, what are we waiting for? Let’s go!

Chapter 1 A Little Give and Take: Mental Addition and Subtraction

Chapter 1

A Little Give and Take:
Mental Addition and Subtraction

For as long as I can remember, I have always found it easier to add and subtract numbers from left to right instead of from right to left. By adding and subtracting numbers this way, I found that I could call out the answers to math problems in class well before my classmates put down their pencils. And I didn’t even need a pencil!

In this chapter you will learn the left-to-right method of doing mental addition and subtraction for most numbers that you encounter on a daily basis. These mental skills are not only important for doing the tricks in this book but are also indispensable in school, at work, or any time you use numbers. Soon you will be able to retire your calculator and use the full capacity of your mind as you add and subtract two-digit, three-digit, and even four-digit numbers with lightning speed.

LEFT-TO-RIGHT ADDITION

Most of us are taught to do math on paper from right to left. And that’s fine for doing math on paper. But if you want to do math in your head (even faster than you can on paper) there are many good reasons why it is better to work from left to right. After all, you read numbers from left to right, you pronounce numbers from left to right, and so it’s just more natural to think about (and calculate) numbers from left to right. When you compute the answer from right to left (as you probably do on paper), you generate the answer backward. That’s what makes it so hard to do math in your head. Also, if you want to estimate your answer, it’s more important to know that your answer is “a little over 1200” than to know that your answer “ends in 8.” Thus, by working from left to right, you begin with the most significant digits of your problem. If you are used to working from right to left on paper, it may seem unnatural to work with numbers from left to right. But with practice you will find that it is the most natural and efficient way to do mental calculations.

With the first set of problems—two-digit addition—the left-to-right method may not seem so advantageous. But be patient. If you stick with me, you will see that the only easy way to solve three-digit and larger addition problems, all subtraction problems, and most definitely all multiplication and division problems is from left to right. The sooner you get accustomed to computing this way, the better.

Two-Digit Addition

Our assumption in this chapter is that you know how to add and subtract one-digit numbers. We will begin with two-digit addition, something I suspect you can already do fairly well in your head. The following exercises are good practice, however, because the two-digit addition skills that you acquire here will be needed for larger addition problems, as well as virtually all multiplication problems in later chapters. It also illustrates a fundamental principle of mental arithmetic—namely, to simplify your problem by breaking it into smaller, more manageable parts. This is the key to virtually every method you will learn in this book. To paraphrase an old saying, there are three components to success—simplify, simplify, simplify.

The easiest two-digit addition problems are those that do not require you to carry any numbers, when the first digits sum to 9 or below and the last digits sum to 9 or below. For example:

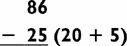
To solve 47 + 32, first add 30, then add 2. After adding 30, you have the simpler problem 77 + 2, which equals 79. We illustrate this as follows:

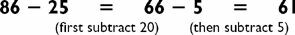
The above diagram is simply a way of representing the mental processes involved in arriving at an answer using our method. While you need to be able to read and understand such diagrams as you work your way through this book, our method does not require you to write down anything yourself.

Now let’s try a calculation that requires you to carry a number:

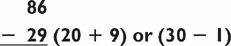
Adding from left to right, you can simplify the problem by adding 67 + 20 = 87; then 87 + 8 = 95.

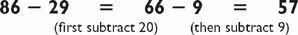
Now try one on your own, mentally calculating from left to right, and then check below to see how we did it:

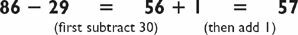
How was that? You added 84 + 50 = 134 and added 134 + 7 = 141.

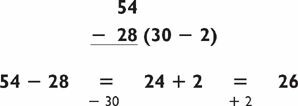
If carrying numbers trips you up a bit, don’t worry about it. This is probably the first time you have ever made a systematic attempt at mental calculation, and if you’re like most people, it will take you time to get used to it. With practice, however, you will begin to see and hear these numbers in your mind, and carrying numbers when you add will come automatically. Try another problem for practice, again computing it in your mind first, then checking how we did it:

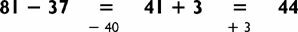
You should have added 68 + 40 = 108, and then 108 + 5 = 113, the final answer. Was that easier? If you would like to try your hand at more two-digit addition problems, check out the set of exercises below. (The answers and computations are at the end of the book.)

Three-Digit Addition

The strategy for adding three-digit numbers is the same as for adding two-digit numbers: you add from left to right. After each step, you arrive at a new (and simpler) addition problem. Let’s try the following:

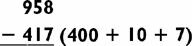
Starting with 538, we add 300, then add 20, then add 7. After adding 300 (538 + 300 = 838), the problem becomes 838 + 27. After adding 20 (838 + 20 = 858), the problem simplifies to 858 + 7 = 865. This thought process can be diagrammed as follows:

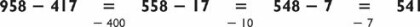
All mental addition problems can be done by this method. The goal is to keep simplifying the problem until you are just adding a one-digit number. Notice that 538 + 327 requires you to hold on to six digits in your head, whereas 838 + 27 and 858 + 7 require only five and four digits, respectively. As you simplify the problem, the problem gets easier!

Try the following addition problem in your mind before looking to see how we did it:

Did you reduce and simplify the problem by adding left to right? After adding the hundreds (623 + 100 = 723), you were left with 723 + 59. Next you should have added the tens (723 + 50 = 773), simplifying the problem to 773 + 9, which you then summed to get 782. Diagrammed, the problem looks like this:

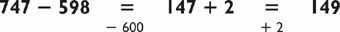
When I do these problems mentally, I do not try to see the numbers in my mind—I try to hear them. I hear the problem 623 + 159 as six hundred twenty-three plus one hundred fifty-nine; by emphasizing the word hundred to myself, I know where to begin adding. Six plus one equals seven, so my next problem is seven hundred and twenty-three plus fifty-nine, and so on. When first doing these problems, practice them out loud. Reinforcing yourself verbally will help you learn the mental method much more quickly.

Three-digit addition problems really do not get much harder than the following:

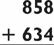
Now look to see how we did it:

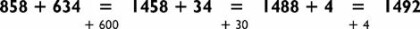
At each step I hear (not see) a “new” addition problem. In my mind the problem sounds like this:

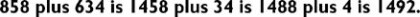
Your mind-talk may not sound exactly like mine (indeed, you might “see” the numbers instead of “hear” them), but whatever it is you say or visualize to yourself, the point is to reinforce the numbers along the way so that you don’t forget where you are and have to start the addition problem over again.

Let’s try another one for practice:

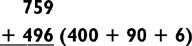
Do it in your mind first, then check our computation below:

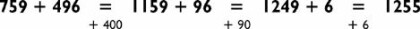
This addition problem is a little more difficult than the last one since it requires you to carry numbers in all three steps. However, with this particular problem you have the option of using an alternative method. I am sure you will agree that it is a lot easier to add 500 to 759 than it is to add 496, so try adding 500 and then subtracting the difference:

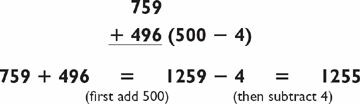
So far, you have consistently broken up the second number in